info@gerb.com
Případová studie tlumicích technologií pro výškové budovy: Komfort a bezpečnost
Pokyny Rady pro výškové budovy a městská obydlí (CTBUH) pro tlumicí systémy
Zkušební věž Thyssen Krupp, Rottweil/Německo
Údaje o projektu
- Rok dokončení:
2016 (vrchol budovy) - Developer/zhotovitel/vlastník:
Krupp Hoesch Stahl GmbH / Thyssen Krupp Elevators - Architekt:
Werner Sobek s ateliéry JAHN Architects ve Stuttgartu a Chicagu - Projektant:
Werner Sobek Stuttgart - Dodavatel tlumicích systémů:
GERB Vibration Control Systems - Zkušební laboratoř:
Wacker Ingenieure (Větrné inženýrství / zkoušky ve větrném tunelu) - Výška / výška mezi podlažími:
246 m / 3,3 m (kancelářské prostory) - Štíhlostní poměr:
1/11,8 - Podlaží:
27 úrovní / 8 podlaží s kancelářskými prostorami - Plocha věže:
340 čtverečních metrů - Funkce budovy:
Zkušební věž pro zkoušky výtahů / kanceláře / vyhlídková plošina (232 m) - Konstrukční materiál:
Železobeton (C50/60) / membránová fasáda z PTFE na ocelové konstrukci - Konstrukční systém:
Konzolové železobetonové jádro na roštovém základu
(- 32 m) - Použitá strategie tlumení:
Hybridní systém tlumení hmotností (240 t)

1.0 Úvod/Historie
V jihozápadním Německu byla postavena 246 metrů vysoká věž, která má sloužit jako zkušební zařízení pro inovace výtahů. Věž má kruhový půdorys o průměru 20 m a poskytuje prostor pro 9 šachet pro zkoušky výtahů, požární výtah a prosklený panoramatický výtah. Kromě toho je k dispozici 220 m šachta, která se používá jako šachta pro mechanické zvedání pro zajištění zkušebních programů.
Základna věže má průměr 40 m, aby poskytla další prostor pro servisní zázemí, vstupní halu a vzdělávací centrum. Vyhlídková plošina ve výšce 232 m – nejvyšší na území Německa – umožňuje nádherný výhled na Černý les a za jasného počasí i na Alpy.

2.0 Konstrukční systém
Konstrukční systém zkušební věže představuje v zásadě železobetonový tubus o průměru 20,8 m, který je upnut 30 metrů do okolní zeminy (viz obrázek 2). Do úrovně 110 m má tubus tloušťku stěn 40 cm a nad ní 25 cm. Zemina, tvořená vrstvou keuperu a pod ní ležícím skořápkovým vápencem, poskytuje vysokou únosnost, takže nebylo nutné použít pilotové založení. Kromě sevření okolní půdou poskytuje širší základová konstrukce věže dodatečnou příčnou tuhost.
Vnitřní vyztužení betonového tubusu je důsledkem především vnitřních stěn výtahových šachet. Pouze na některých výškových úrovních byly nainstalovány prefabrikované stropní desky, aby byl umožněn přístup k výtahovým šachtám. Některé výtahové šachty končí ve výšce 115 m a jsou zakryty 40 cm silnými podlahami s dlouhým rozpětím, které byly odlity přímo na místě. Tyto podlahy se používají v kancelářských prostorách. Nad nimi se nachází prázdný prostor do výšky 197 m, který slouží jako zásobník tepla a pro systém TMD. V horní části věže jsou kancelářské prostory a zbývající výtahové šachty.

Charakteristickým rysem testovací věže je textilní fasáda, kterou tvoří síťovina ze skelných vláken potažená PTFE. Šířka otvorů síťoviny se s výškou budovy zvětšuje, aby se zvýšila průsvitnost fasády, snížila hustota a hmotnost materiálu a posílily se aerodynamické účinky.
Spirálovitý tvar fasády má fungovat jako tzv. Scrutonova spirála a samotná tkanina pomáhá stínit betonovou konstrukci, aby se zabránilo tepelnému namáhání způsobenému slunečním zářením. Při návrhu fasády a výběru materiálu bylo třeba zohlednit aspekty instalace, údržby a trvanlivosti, ovšem navíc i zatížení větrem.
3.0 Postup výstavby

Stavba zkušební věže proběhla v následujících krocích:
- Vyhloubení 30 m hluboké kruhové stavební jámy pro základnu věže. Výkopu a jeho tvaru bylo dosaženo odstřelem na začátku. Po výkopu byla jáma zajištěna zemními kotvami a ostěním ze vstřikovaného betonu.
- Vylití roštových základů
- Výstavba svislé betonové konstrukce s použitím posuvného bednění. Všechny stěny se stavěly nepřetržitě po dobu 4 měsíců.
- Výstavba podlahových desek
- Výstavba vstupního prostoru
4.0 Předpokládaná dynamická citlivost na zatížení větrem
Základní frekvence pro zkušební věž byly předpokládány v rozmezí 0,17– 0,20 Hz v závislosti na fázi výstavby a stavu betonu (popraskaný/nepopraskaný) – viz obrázek 4.
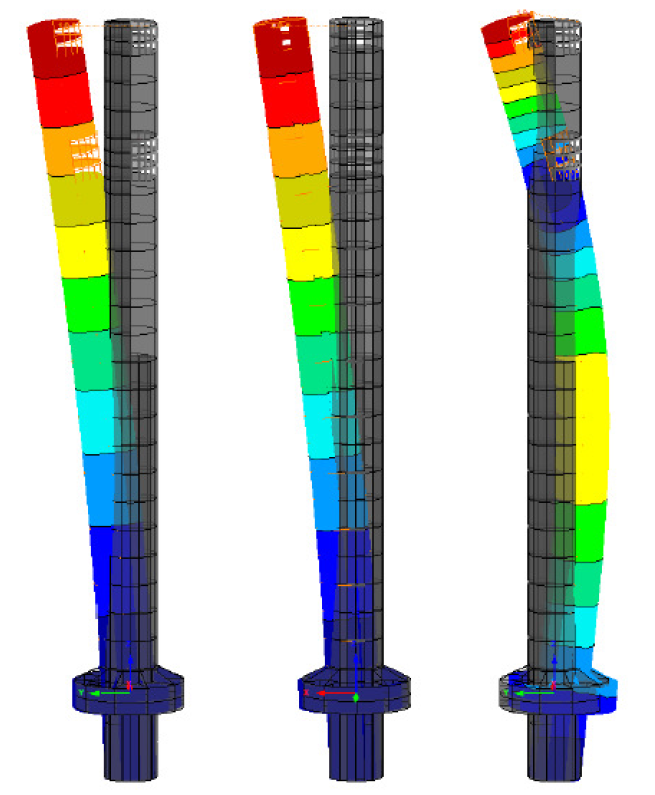
Analýza větru ukázala, že k rezonančnímu buzení konstrukce může docházet při rychlostech větru, které odpovídají hodnotám při zemi (výška 10 m) v rozmezí 55–60 km/h. Předpokládalo se, že bez dodatečného tlumení by toto rezonanční buzení způsobilo odchylky horní části věže přibližně +/- 750 mm, což by nejen způsobilo nepohodlí uživatelům, ale mělo by to také významné důsledky pro únavovou životnost betonové konstrukce věže (viz obrázek 5). Z důvodu snížení dynamické citlivosti na boční vítr byl realizován pasivní systém tlumiče vibrací. Vzhledem k tomu, že věž má být používána jako zkušební věž pro výtahová zařízení citlivá na kývání, hledal vlastník možnost,
jak věž vybudit uměle v klidných dnech, avšak s posunem, který by nezpůsobil žádné problémy s únavou konstrukce či materiálu. Požadovaná úroveň umělého kývavého pohybu se pohybovala v bezpečném rozmezí, přibližně +/- 200 mm. Tento požadavek poskytl vzácnou příležitost realizovat hybridní systém tlumiče hmotností (HMD) nebo, protože se konstrukční systém odchyluje od jiných systémů HMD, které byly vyrobeny v minulosti, takzvaný systém TMD s duálním použitím. Systém bude představen v následujících kapitolách, včetně optimalizace pasivního systému, návrhu mechanismu aktuátorů, řídicích algoritmů a koncepce bezpečnosti.

5.0 Optimalizace pasivního systému tlumiče vibrací
Parametry pasivního systému TMD musely být stanoveny s ohledem na tři různé aspekty: a) zajištění dostatečného dodatečného tlumení konstrukce, aby se snížila dynamická citlivost v důsledku buzení víry; b) omezení výsledný posun hlavní hmoty TMD v pasivním režimu na dosažitelnou/praktickou hodnotu při buzení nárazovým větrem a c) zvolení hmoty TMD podle příkonu energie, který je nutný pro požadovaný maximální odklon věže v režimu buzení, s ohledem na její účinnou plochu, což umožňují použité aktuátory
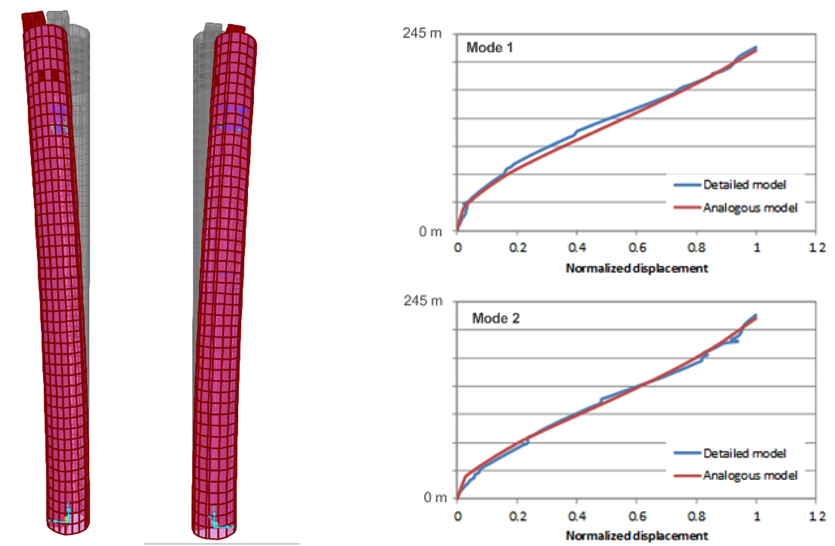
(tj. maximální vygenerovaná síla a maximální zdvih během provozu). K optimalizaci systému TMD byl použit numerický model, který reprezentoval rozložení hmotnosti věže a momenty setrvačnosti, jak jsou uvedeny v identifikovaných vlastnostech konstrukce. Prvky tuhosti mezi podlahami byly rovněž přizpůsobeny tak, aby odpovídaly tvarům módů a vlastním frekvencím z pozorování v plném měřítku. Na obr. 6 vlevo jsou znázorněny tvary módů a vlastní frekvence tohoto použitého analogického modelu. Na obr. 6 vlevo jsou také porovnány tvary módů analogického modelu s tvary detailního modelu připraveného poradcem pro konstrukční řešení.
Kromě toho byl realizován diskrétní model TMD jako kyvadlový systém zachycující i jeho excentrickou polohu na věži. Charakteristiky zatížení pro rozhodný vstupní případ, tj. rezonanční buzení způsobené vířením, jsou velmi podobné charakteristikám pro harmonické buzení z jednoho směru. Současné zatížení poryvy větru je však ze své podstaty stochastické (náhodné) povahy a platí pro něj jiná optimalizační kritéria než známé Den Hartogovo kritérium. Kromě toho jsou relativní posuny hmoty TMD větší u stochastického než u harmonického typu zatížení. Vzhledem k tomu, že pro číselné stanovení optimálních parametrů systému TMD je třeba zvažovat zatížení blízké realitě, byl vygenerován časový průběh, který zahrnoval jak stochastické zatížení poryvy (založené na Davenportově spektru), tak superponovanou rezonanční složku podobnou víření, která představuje celkové buzení bočním větrem (viz obr. 3 vpravo). Snížení odchylky věže, kterého lze dosáhnout pomocí optimalizovaného pasivního systému TMD, a výsledné posuny TMD jsou znázorněny na obr. 3 vpravo.
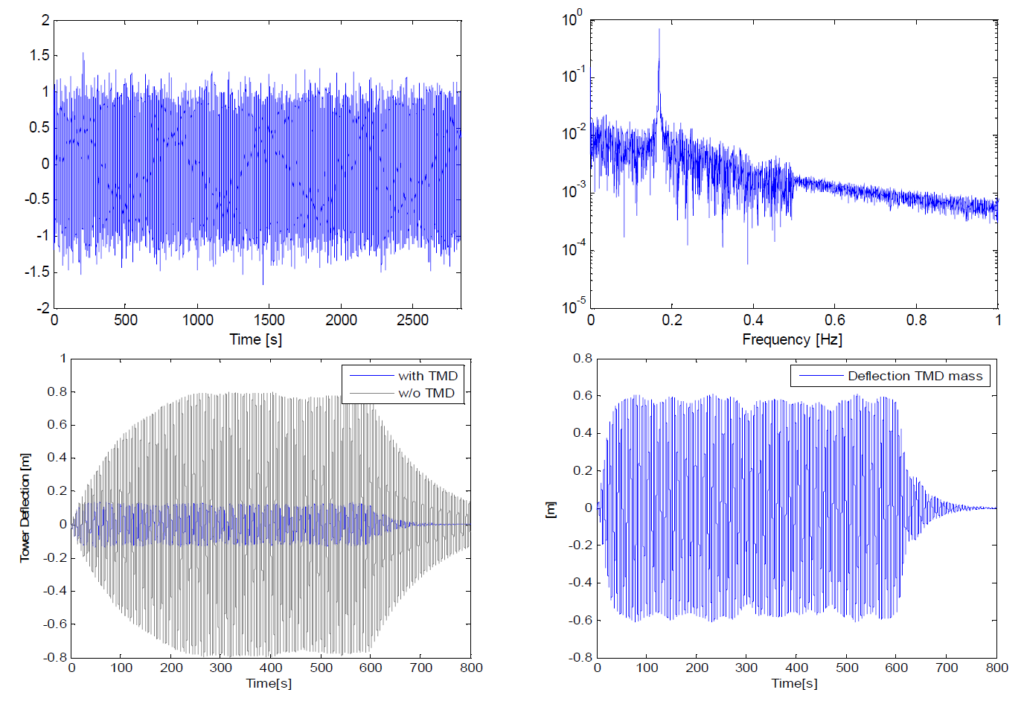
Na základě těchto výsledků pro odhadované vlastní tlumení konstrukce ξ = 0,8 % bylo zjištěno, že pro udržení posunů v rozmezí +/- 650 mm při zachování optimálního poměru tlumení TMD pro nejlepší výkon TMD je nutná hmotnost systému TMD 240 t. Zvýšení tlumení TMD by mohlo zkrátit dráhu, přičemž účinnost by byla stále dostatečná, ale to by nepříznivě ovlivnilo požadavky na sílu aktuátoru. Pro určení potřebných sil pro optimální nastavení 240t systému TMD byl použit také analogický model, který ověřil, že při maximální síle 40 kN z aktuátorů lze dosáhnout vychýlení věže v rozmezí +/- 200 mm. Na obr. 4 jsou zobrazeny výsledky numerické simulace v časové oblasti na analogickém numerickém modelu; v tomto případě jsou zobrazeny výsledné odchylky vrcholu věže, výchylky hmoty TMD a aktivní vstupní síly, které je způsobují.


6.0 Popis systému
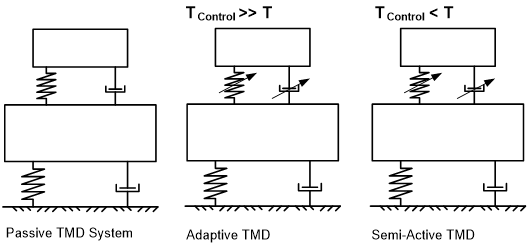
Dualita řídicího systému slouží a) ke snížení spotřeby energie při běžném pasivním provozu, aby se snížily vznikající vibrace; b) ke snížení požadavků na sílu pro aktuátory díky využití rezonančních efektů k vybuzení hlavní hmoty TMD, aby nakonec bylo dosaženo skutečné požadované síly. V porovnání s jinými řídicími systémy (viz obr. 1) tedy aktuátory spojují hlavní konstrukci a hmotu systému TMD, ale nepoužívají se k přímému ovládání hmoty TMD, jak by tomu bylo v případě typického systému aktivního systému regulace hmoty (Active Mass Driver)/tlumič.
Pro realizovaný TMD s duálním použitím byla zvolena reakční hmotnost pro pasivní provoz 240 tun. V režimu buzení jsou k TMD připojeny dva lineární pohony – v každém hlavním směru jeden – s čepy v blízkosti těžiště hmoty, aby se zabránilo vzniku torzních odchylek. Každý lineární pohon může vyvinout sílu až 40 kN při zdvihu max. +/- 600 mm (viz detail na obr. 2). Lineární pohony lze odpojit, takže celý pasivní režim nebude ovlivněn ložisky aktuátorů z důvodu zabránění nepravděpodobnému případu poruchy ložisek.
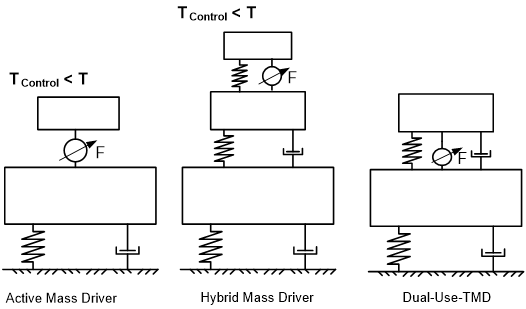
Obrázek 10 – Typy TMD systémů – TMD s duálním použitím v porovnání s pasivními, poloaktivními, aktivními a hybridními systémy
Systém je vybaven čtyřmi jednoosými akcelerometry (seismický K-Beam/MEMS; v každém směru jeden) pro určení zrychlení horní úrovně věže a hmotnosti TMD. Signály zrychlení se filtrují podle pásma uvnitř frekvenčního rozsahu základních přirozených frekvencí věže (0,1–0,3 Hz) a integrují se, aby se získaly rychlosti a odchylky věže.
Kromě toho lze integrované hodnoty posunutí porovnat s hodnotami doplňkového globálního navigačního satelitního systému instalovaného rovněž na vrcholu, aby bylo možné porovnat odchylky signálu. V souladu s tím byly provedeny počáteční korelační testy. Kromě toho se posuny TMD monitorují přímo pomocí snímačů strunového potenciometru a indukčního systému měření délky integrovaného v lineárních motorech.
7.0 Řídicí algoritmus
Obecná regulační smyčka pro věž je znázorněna na obr. 5, kde je znázorněna sekvence řízení v uzavřené smyčce. Podrobný návrh řídicího algoritmu by vyžadoval analytické modely interakce mezi akčními a hmotou TMD, aby bylo možné určit souvislost mezi vstupem akčního členu a působící silou. Ty by se měly kombinovat s analytickým modelem hlavní konstrukce, který popisuje celkové dynamické chování budovy. V porovnání se standardními řídicími algoritmy, které byly použity v jiných aplikacích HMD, např. v [2],[3] nebo byly teoreticky zkoumány, např. v [1] Algoritmus pro tuto aplikaci musel pro věž zohlednit synchronní řízené buzení v jednom hlavním směru a snížení vibrací v kolmém směru. Vzhledem k tomu, že dynamická citlivost se očekává především v základních režimech, lze pro obě tyto úlohy použít lineární řízení se zpětnou vazbou se všemi jeho výhodami s ohledem na zamezení nestabilitám. Pro použitou jednoduchou realizaci platí, že lineární systém, který tlumí dynamickou citlivost věže kolmo na buzení, řídí příslušný aktuátor prostřednictvím zadaného váženého lineárního součtu sedmi měření dynamiky konstrukce. Jde o měření: zrychlení TMD a vrcholu věže, rychlosti TMD a vrcholu věže, posuny TMD a vrcholu věže a relativní posun TMD vůči vrcholu věže.
Je důležité poznamenat, že předem zvolené faktory vážení jsou jednoduché, kladné nebo záporné skalární zisky. Parametrizace faktorů vážení vychází z dynamických zkoušek věže a nepoužívá žádné úpravy závislé na frekvenci. Zpětná vazba aktivního aktuátoru se počítá okamžitě (při 50 Hz) a je opět lineární kombinací předchozích dynamických měření. Nepoužívá se žádná nelineární manipulace. Návrh řízení byl také implementován do numerické simulace v časové oblasti (tj. přímá integrace), aby se prokázala výkonnost řízení aktuátoru pro zmírnění vibrací. Pro režim buzení byl použit stejný přístup v kombinaci s posunem měřené konstrukce, který představuje vybuzení věže na požadovanou hodnotu odchylky. Posun je sinusová funkce založená na zjištěné základní frekvenci každého směru. Řídicí výstup pro potlačení změn horního průhybu způsobených jinými narušeními je poté modulován na sinusové funkci posunu a hodnota regulace se odpovídajícím způsobem upraví.
Lineární řízení se zpětnou vazbou pro snížení dynamické citlivosti věže kolmo na buzení umožňuje, aby silový povel pro pohon byl zadaným váženým lineárním součtem sedmi dynamických měření programu. Těchto sedm měření je: zrychlení TMD a věže, rychlost TMD a věže, posun TMD a věže a relativní posun TMD vůči věži. Je důležité poznamenat, že faktory vážení jsou jednoduché, kladné nebo záporné skalární hodnoty. Parametrizace faktoru vážení vychází z experimentálních dynamických zkoušek věže. Zpětná vazba aktuátoru je aktivní, počítá se okamžitě (50 Hz)
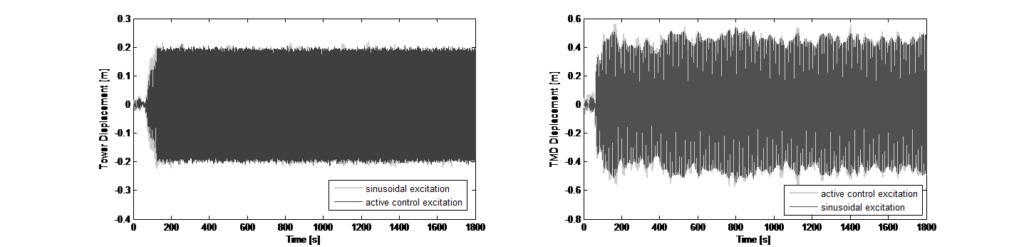
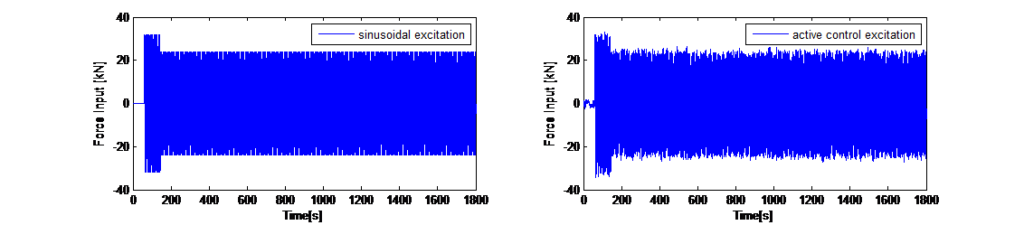
a faktory vážení jsou skalární hodnoty, které nepoužívají žádnou formu funkce přenosu závislé na frekvenci. Také zpětná vazba je lineární kombinací dynamické vlastnosti. Nepoužívá se žádná nelineární manipulace an nelinární logika. Návrh řízení byl implementován pro numerickou simulaci v časové oblasti (přímá integrace), takže pro každý časový krok bylo možné přizpůsobit silový vstup do hmoty TMD jako řízení aktuátoru. Na obrázku 12 jsou uvedeny výsledky simulace pro potlačení vibrací – posuny věže a výsledná dráha TMD.
Pro režim buzení byl použit stejný přístup v kombinaci s posunem měřené konstrukce, který představuje vybuzení věže na požadovanou hodnotu odchylky. Posun je sinusová funkce založená na zjištěné základní frekvenci pro každý směr. Řídicí výstup pro potlačení změn horní odchylky způsobené narušením je poté modulován na sinusové funkci
posunu a hodnotu regulace je nutno odpovídajícím způsobem upravit. Pro tento posun experimentálně určen faktor vážení. Na obrázku 13 jsou zobrazeny číselné výsledky s rušivým nárazovým zatížením pro režim buzení s jednoduchým sinusovým buzením a s použitým řídicím algoritmem.
8.0 Koncepce bezpečnosti
Vzhledem k síle +/- 40 kN, kterou mohou vyvinout lineární pohony používané jako aktuátory, je nezbytná koncepce bezpečnosti, která zajistí, že posuny věže nepřekročí ustanovení ohledně únavy konstrukce a materiálu. To platí i přesto, že výstupní síla není dostatečná k tomu, aby způsobila odchylku horní části větší než předem stanovených +/-200 mm. Jedním z přístupů ke zvýšení bezpečnosti systému bylo zvýšení redundance monitorovacích snímačů, které zaznamenávají průhyb horní části věže. Toho lze nejlépe dosáhnout implementací dalšího nezávislého monitorovacího systému, který v ideálním případě používá jiný měřicí princip než vlastní řídicí hardware. Pro zde prezentovaný projekt byly v řídicím hardwaru použity akcelerometry a definovaný práh zrychlení pro pásmovou filtraci signálu v rozsahu příslušných přirozených frekvencí konstrukce. Nadřazeným monitorovacím systémem je globální družicový navigační systém (GNSS) s přesností +/- 10 mm.
Monitorovací systém GNNS vyžaduje referenční základnovou stanici, která zpracovává souřadnicová data na skutečné hodnoty odezvy na posun. Pokud odchylka vrcholu věže během režimu umělého buzení překročí předem stanovenou mez, což by mohlo být způsobeno dalším větrem nebo jiným buzením, relé přepne signál detekce přítomnosti na 0 V. To způsobí přerušení režimu buzení. Kromě toho oba monitorovací systémy neustále kontrolují získaná data, zda nedošlo k výskytu chybných signálů ze snímačů, což rovněž vede k přerušení aktivního režimu buzení. Chybné signály zrychlení / strunového potenciometru budou detekovány pomocí kritéria výběru spektrálních špiček – pouze pokud lze možné vybrat špičku v příslušném rozsahu, lze předpokládat, že snímače poskytují legitimní signály. Monitorovací systém GNNS analyzuje změnu souřadnicových dat, ovšem pokud se vzorkovaná data včas nezmění, automaticky se předpokládá chybný signál.
9.0 Vibrační zkoušky
Počáteční vibrační zkoušky věže byly provedeny v současné fázi, kdy věž ještě není dokončena, takže základní frekvence věže v této fázi jsou nad stanoveným rozsahem ladění pasivního systému TMD. Systém TMD je nastaven na nejvyšší možnou frekvenci ladění. Cílem vibračních zkoušek bylo stanovení základních frekvencí věže se zablokovaným systémem TMD a vlastního tlumení konstrukce. Dále by se mělo stanovit dynamické chování s aktivovaným pasivním systémem TMD a zvýšení tlumení konstrukce vlivem pasivního systému TMD. K určení základních přirozených frekvencí věže lze použít metodu zprůměrované normalizované spektrální hustoty výkonu [1] (ANPSD). Za tímto účelem je zaznamenané časové průběhy nutno rozdělit do segmentů. Tyto segmenty je nutno převést do frekvenční oblasti. Výsledná spektra je nutno normalizovat, zprůměrovat a vynásobit komplexně konjugovanými spektry.
Tím se odstraní všechny náhodné vibrace a ve zprůměrovaném spektru se zobrazí pouze opakující se volné vibrace konstrukce, které nyní představují dominantně buzené přirozené frekvence věže. Na obrázku 14 vlevo jsou zobrazeny zaznamenané časové průběhy vodorovných vibrací okolí ve směrech x a y při zablokovaném systému TMD. Na obrázku 14 vlevo jsou zobrazena výsledná zprůměrovaná automatická spektra výkonu pro úsek o délce 120 sekund. Spektra ukazují, že věž vykazuje dynamickou odezvu ve dvou dominantních frekvencích (0,225 Hz ve směru x a 0,245 Hz ve směru y).
V návaznosti na výše popsanou metodu zprůměrovaného spektra výkonu – která předpokládá, že okolní buzení způsobuje dostatečnou dynamickou odezvu v zájmových módech vibrací, aby bylo dosaženo stochastické bezpečnosti – byly vlastní frekvence určeny pomocí komerčního softwaru pro zpracování signálů ARTEMIS, [1] který zahrnuje metody rozšířené dekompozice frekvenční oblasti a stochastické identifikace podprostoru.
Metody rozšířená dekompozice ve frekvenční oblasti (EFDD) a stochastické identifikace podprostoru jsou široce používané techniky pro identifikaci modálních parametrů výhradně na výstupu.
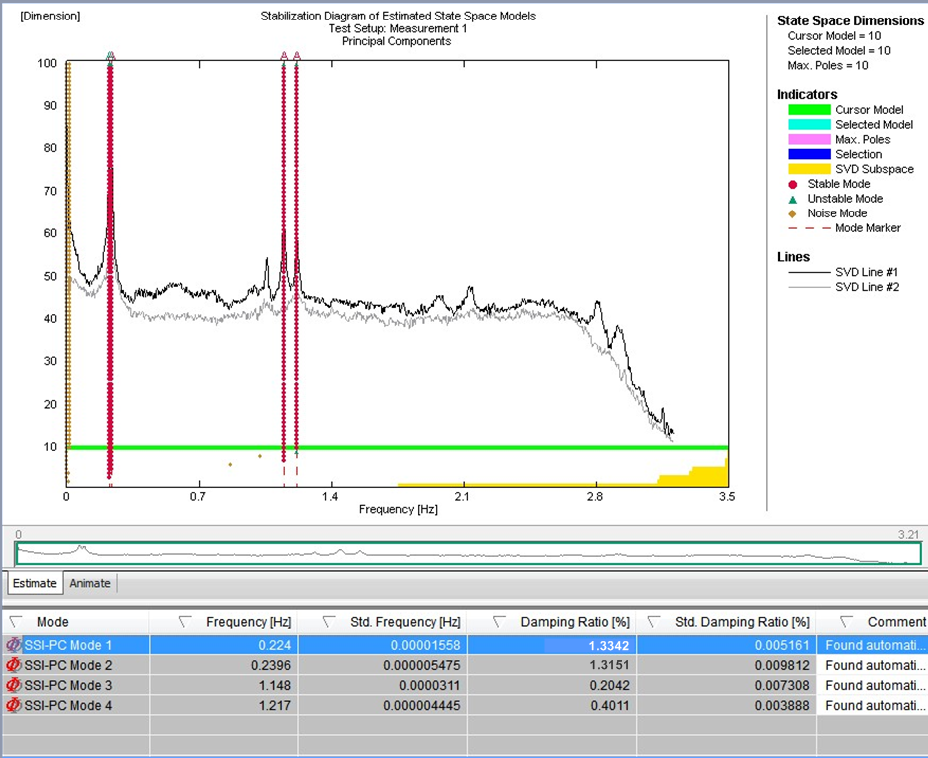
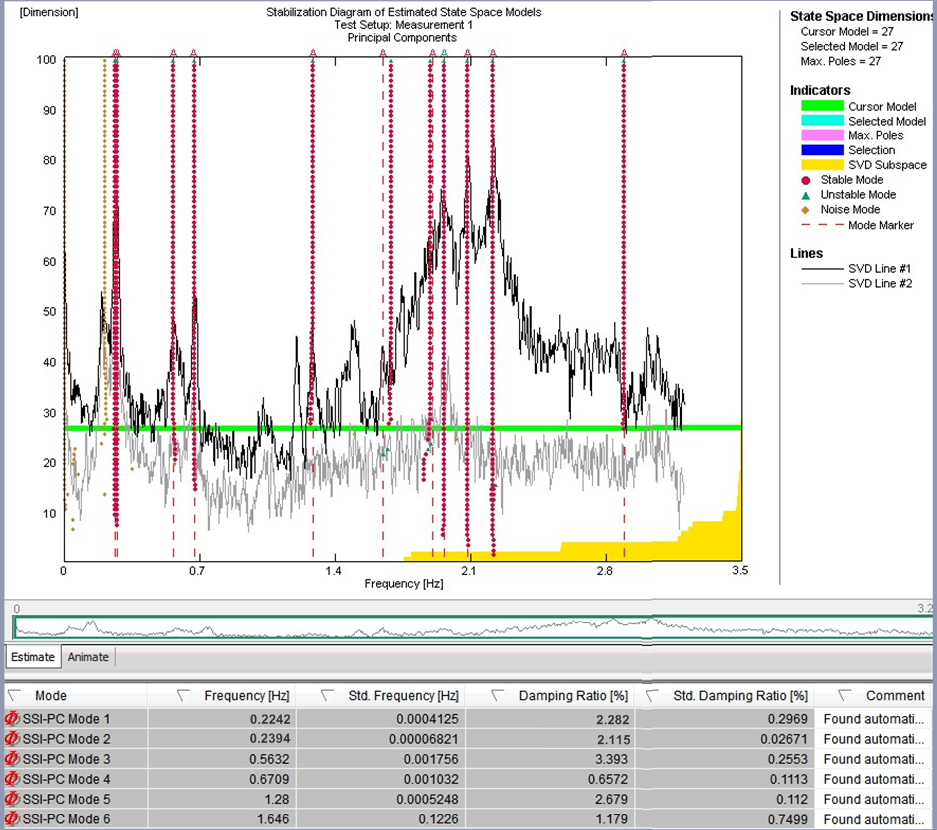
Obrázek 15 – Karty stability pro záznam okolních vibrací se zablokovaným systémem TMD (vlevo) a aktivovaným systémem TMD (vpravo)
Metoda EFDD je založena na výpočtu spekter odezvy. Pro udržení nízké úrovně chyby odhadu spektra a spolehlivou extrakci modálních parametrů jsou proto nutné dlouhé záznamy. K identifikaci mostů pomocí modelu založeného výhradně na výstupu byl použit algoritmus stochastické identifikace podprostoru. Metody stochastické identifikace podprostoru fungují v časové oblasti a jsou založeny na popisu dynamického problému ve stavovém prostoru. Výsledky identifikace systému při různých řádech modelu se porovnávají za účelem rozlišení skutečných strukturálních módů od falešných módů v tzv. stabilizačních diagramech. Tyto diagramy jsou oblíbeným způsobem výběru identifikovaného modelu systému, protože skutečné strukturální módy mají tendenci být stabilní pro po sobě následující pořadí modelu a splňují určitá stabilizační kritéria, která se vyhodnocují automatizovaným postupem. Na obrázku 15 je zobrazena výsledná karta stability pro zaznamenaná data z okolí, z níž bylo možné určit příslušné módy. Identifikované módy a stanovené poměry tlumení pro jednotlivé módy ve stavu se zablokovaným systémem TMD (vlevo) a se zapnutým systémem TMD (vpravo) jsou rovněž zobrazeny na obrázku 14. Je patrné zvýšení tlumení konstrukce. Dodatečné tlumení konstrukce se pohybuje v rozmezí teoretické hodnoty, kterou lze určit z teoretického modelu, pro který bylo uvažováno nevyladěné nastavení systému TMD.
Kromě testů okolních vibrací s pasivním systémem TMD byly provedeny předběžné testy s aktivním režimem buzení, a to i přes nevyladěný stav systému TMD. Obrázek 12 vlevo ukazuje časový průběh zaznamenaných zrychlení na vrcholu věže. Po počátečním sinusovém buzení bylo možné pomocí algoritmu pro ustálenou úroveň zrychlení experimentálně určit korelaci mezi průhybem věže a nuceným posunem hmoty systému TMD. Časový průběh na obrázku 12 zobrazuje oba zkušební scénáře v režimu buzení a odpovídající spektra FFT ukazují jasnou odezvu věže v jejích dvou základních frekvencích (směr x a y). Zeleně vyznačený časový úsek představuje sinusové buzení hmoty s vypnutým aktivním řízením, které způsobilo dynamickou odezvu v obou hlavních směrech. Výsledné spektrum FFT zobrazuje dvě špičky pro identifikaci základních frekvencí v těchto dvou směrech. Modře vyznačený časový úsek je pro buzení s povoleným aktivním řízením, které způsobilo stabilnější posun věže převážně v jednom směru. Výsledný útlum vibrací po vypnutí režimu buzení byl rovněž použit k určení tlumení konstrukce a byl stanoven na D = 2,4 %. Tento výsledek koreluje s poměrem tlumení určeným pomocí algoritmů SSI.
10.0 Závěr a výhled
Ve 246 m vysoké zkušební věži Thyssen Krupp byl instalován systém TMD s duálním použitím, jehož cílem je úmyslně vybuzovat věž na řízenou dynamickou odezvu v jejích základních frekvencích. Cílem tohoto buzení je dosáhnout definovaných výkyvů budovy ve dvou hlavních směrech věže. Na základě numerických výpočtů bylo zjištěno, že k dosažení požadovaného přídavného tlumení pro pasivní režim a k vytvoření požadované síly pro dosažení posunu vrcholu věže +/- 200 mm je zapotřebí systém TMD 240 t. Pro vytvoření ustálené úrovně posunu pro režim buzení a potlačení posunů způsobených větrem a vynucenou složkou vibrací v kolmém směru byl vyvinut řídicí algoritmus, který byl testován s použitím numerických simulací. Po instalaci pasivního systému TMD kyvadlového typu, pro který byly jako reakční hmota použity prefabrikované betonové desky, byly aktuátory uvedeny do provozu a byly provedeny první zkoušky. Zkoušky ukázaly, že vlastní tlumení věže je vyšší, než se předpokládalo, ale že lze jasně určit všechny relevantní módy. Aktivní režim buzení budovy funguje a bylo ho možno otestovat, i když nikoli v plném rozsahu, aby bylo možné odvodit všechny provozní parametry, protože budova ještě není zcela dokončena. Vzhledem k nedokončenosti budovy nebylo možno přizpůsobit pasivní systém TMD stanoveným základním frekvencím.
Jakmile bude systém TMD upraven, budou provedeny další zkoušky budovy, které budou zahrnovat také zkoušky amplitudově závislých tlumicích vlastností a integrity koncepce bezpečnosti.
REFERENCE
[1] Wenzel, H., Pichler, D., Schedler, R. (1991). „Ambiente Schwingungsmessungen zur System und Schadenserkennung an Tragwerken“, Bauingenieur 74
[2] Döhler, M., Andersen, P.: Mevel, L. (2012). „Operational Modal Analysis using a Fast Stochastic Subspace Identification Method“, Sborník z řady konferencí Společnosti pro experimentální mechaniku (Society for Experimental Mechanics)
[3] Soong, T. T., Spencer, J. R. (2000). „Active, Semi-Active and hybrid control of structures“ na 12. světové konferenci pro zemětřesné inženýrství
[4] Ricciardelli, F.; Pizzimenti, A.D.; Mattei, M. (2003). Pasivní i aktivní TMD jako řešení větrných podmínek výškových staveb. Eng. Struct., 25, 1199–1209
[5] Yang, N.Y.; Agrawal, A.K.; Samali, B.; Wu, J.C. Benchmark Problem for Response Control of Wind-Excited Tall Buildings. J. Eng. Mech. 2004, 130, 437–446.
[6] Watakabe, M.; Tohdp, M.; Chiba, O.; Izumi, N.; Ebisawa, H.; Fujita, T. Response control performance of a hybrid mass damper applied to a tall building. Earthq. Eng. Struct. Dyn. 2001, 30, 1655–1676.
[7] Tan, P.; Liu, Y.; Zhou, F.; Teng, J. Hybrid Mass Dampers for Canton Tower. CTBUH J. 2012, 24–29.
[8] Soong, T. T. „Active Structural Control: Theory and Practice“; John Wiley & Sons, Inc.: New York, NY, USA, 1990
[9] Preumont, A., Kazuto, S. (2008). „Active Control of Structures“, Wiley, Padstow
Další zdroje
Potřebujete další informace o tomto tématu?
Neváhejte se na nás obrátit s konkrétním dotazem.
Jeden z našich projektových inženýrů se vám brzy ozve.
Případová studie tlumicích technologií pro výškové budovy: Komfort a bezpečnost
Pokyny Rady pro výškové budovy a městská obydlí (CTBUH) pro tlumicí systémy
Zkušební věž Thyssen Krupp, Rottweil/Německo
Údaje o projektu
- Rok dokončení:
2016 (vrchol budovy) - Developer/zhotovitel/vlastník:
Krupp Hoesch Stahl GmbH / Thyssen Krupp Elevators - Architekt:
Werner Sobek s ateliéry JAHN Architects ve Stuttgartu a Chicagu - Projektant:
Werner Sobek Stuttgart - Dodavatel tlumicích systémů:
GERB Vibration Control Systems - Zkušební laboratoř:
Wacker Ingenieure (Větrné inženýrství / zkoušky ve větrném tunelu) - Výška / výška mezi podlažími:
246 m / 3,3 m (kancelářské prostory) - Podlaží:
27 úrovní / 8 podlaží s kancelářskými prostorami - Plocha věže:
340 čtverečních metrů - Funkce budovy:
Zkušební věž pro zkoušky výtahů / kanceláře / vyhlídková plošina (232 m) - Použitá strategie tlumení:
Hybridní systém tlumení hmotností (240 t)

- Konstrukční materiál:
Železobeton (C50/60) / membránová fasáda z PTFE na ocelové konstrukci - Konstrukční systém:
Konzolové železobetonové jádro na roštovém základu
(- 32 m)
Případová studie tlumicích technologií pro výškové budovy: Komfort a bezpečnost
Pokyny Rady pro výškové budovy a městská obydlí (CTBUH) pro tlumicí systémy
Zkušební věž Thyssen Krupp, Rottweil/Německo
Údaje o projektu
- Rok dokončení: 2016 (vrchol budovy)
- Developer/zhotovitel/vlastník: Krupp Hoesch Stahl GmbH / Thyssen Krupp Elevators
- Architekt: Werner Sobek s ateliéry JAHN Architects ve Stuttgartu a Chicagu
- Projektant: Werner Sobek Stuttgart
- Dodavatel tlumicích systémů: GERB Vibration Control Systems
- Zkušební laboratoř: Wacker Ingenieure (Větrné inženýrství / zkoušky ve větrném tunelu)
- Výška / výška mezi podlažími: 246 m / 3,3 m (kancelářské prostory)
- Podlaží: 27 úrovní / 8 podlaží s kancelářskými prostorami
- Plocha věže: 340 čtverečních metrů
- Funkce budovy: Zkušební věž pro zkoušky výtahů / kanceláře / vyhlídková plošina (232 m)
- Konstrukční materiál: Železobeton (C50/60) / membránová fasáda z PTFE na ocelové konstrukci
- Konstrukční systém: Konzolové železobetonové jádro na roštovém základu (- 32 m)
- Použitá strategie tlumení: Hybridní systém tlumení hmotností (240 t)

1.0 Úvod/Historie
V jihozápadním Německu byla postavena 246 metrů vysoká věž, která má sloužit jako zkušební zařízení pro inovace výtahů. Věž má kruhový půdorys o průměru 20 m a poskytuje prostor pro 9 šachet pro zkoušky výtahů, požární výtah a prosklený panoramatický výtah. Kromě toho je k dispozici 220 m šachta, která se používá jako šachta pro mechanické zvedání pro zajištění zkušebních programů.
Základna věže má průměr 40 m, aby poskytla další prostor pro servisní zázemí, vstupní halu a vzdělávací centrum. Vyhlídková plošina ve výšce 232 m – nejvyšší na území Německa – umožňuje nádherný výhled na Černý les a za jasného počasí i na Alpy.

2.0 Konstrukční systém
Konstrukční systém zkušební věže představuje v zásadě železobetonový tubus o průměru 20,8 m, který je upnut 30 metrů do okolní zeminy (viz obrázek 2). Do úrovně 110 m má tubus tloušťku stěn 40 cm a nad ní 25 cm. Zemina, tvořená vrstvou keuperu a pod ní ležícím skořápkovým vápencem, poskytuje vysokou únosnost, takže nebylo nutné použít pilotové založení. Kromě sevření okolní půdou poskytuje širší základová konstrukce věže dodatečnou příčnou tuhost.
Vnitřní vyztužení betonového tubusu je důsledkem především vnitřních stěn výtahových šachet. Pouze na některých výškových úrovních byly nainstalovány prefabrikované stropní desky, aby byl umožněn přístup k výtahovým šachtám. Některé výtahové šachty končí ve výšce 115 m a jsou zakryty 40 cm silnými podlahami s dlouhým rozpětím, které byly odlity přímo na místě. Tyto podlahy se používají v kancelářských prostorách. Nad nimi se nachází prázdný prostor do výšky 197 m, který slouží jako zásobník tepla a pro systém TMD. V horní části věže jsou kancelářské prostory a zbývající výtahové šachty.

Charakteristickým rysem testovací věže je textilní fasáda, kterou tvoří síťovina ze skelných vláken potažená PTFE. Šířka otvorů síťoviny se s výškou budovy zvětšuje, aby se zvýšila průsvitnost fasády, snížila hustota a hmotnost materiálu a posílily se aerodynamické účinky.
Spirálovitý tvar fasády má fungovat jako tzv. Scrutonova spirála a samotná tkanina pomáhá stínit betonovou konstrukci, aby se zabránilo tepelnému namáhání způsobenému slunečním zářením. Při návrhu fasády a výběru materiálu bylo třeba zohlednit aspekty instalace, údržby a trvanlivosti, ovšem navíc i zatížení větrem.
3.0 Postup výstavby

Stavba zkušební věže proběhla v následujících krocích:
- Vyhloubení 30 m hluboké kruhové stavební jámy pro základnu věže. Výkopu a tvaru bylo dosaženo odstřelem na začátku. Po výkopu byla jáma zajištěna zemními kotvami a ostěním ze vstřikovaného betonu.
- Vylití roštových základů
- Výstavba svislé betonové konstrukce s použitím posuvného bednění. Všechny stěny se stavěly nepřetržitě po dobu 4 měsíců.
- Výstavba podlahových desek
- Výstavba vstupního prostoru
4.0 Předpokládaná dynamická citlivost na zatížení větrem
Základní frekvence pro zkušební věž byly předpokládány v rozmezí 0,17– 0,20 Hz v závislosti na fázi výstavby a stavu betonu (popraskaný/nepopraskaný) – viz obrázek 4.

Analýza větru ukázala, že k rezonančnímu buzení konstrukce může docházet při rychlostech větru, které odpovídají hodnotám při zemi (výška 10 m) v rozmezí 55–60 km/h. Předpokládalo se, že bez dodatečného tlumení by toto rezonanční buzení způsobilo odchylky horní části věže přibližně +/- 750 mm, což by nejen způsobilo nepohodlí uživatelům, ale mělo by to také významné důsledky pro únavovou životnost betonové konstrukce věže (viz obrázek 5). Z důvodu snížení dynamické citlivosti na boční vítr byl realizován pasivní systém tlumiče vibrací. Vzhledem k tomu, že věž má být používána jako zkušební věž pro výtahová zařízení citlivá na kývání, hledal vlastník možnost, jak věž vybudit uměle v klidných dnech, avšak s posunem, který by nezpůsobil žádné problémy s únavou konstrukce či materiálu. Požadovaná úroveň umělého kývavého pohybu se pohybovala v bezpečném rozmezí, přibližně +/- 200 mm. Tento požadavek poskytl vzácnou příležitost realizovat hybridní systém tlumiče hmotností (HMD) nebo, protože se konstrukční systém odchyluje od jiných systémů HMD, které byly vyrobeny v minulosti, takzvaný systém TMD s duálním použitím. Systém bude představen v následujících kapitolách, včetně optimalizace pasivního systému, návrhu mechanismu aktuátorů, řídicích algoritmů a koncepce bezpečnosti.

5.0 Optimalizace pasivního systému tlumiče vibrací
Parametry pasivního systému TMD musely být stanoveny s ohledem na tři různé aspekty: a) zajištění dostatečného dodatečného tlumení konstrukce, aby se snížila dynamická citlivost v důsledku buzení víry; b) omezení výsledný posun hlavní hmoty TMD v pasivním režimu na dosažitelnou/praktickou hodnotu při buzení nárazovým větrem a c) zvolení hmoty TMD podle příkonu energie, který je nutný pro požadovaný maximální odklon věže v režimu buzení, s ohledem na její účinnou plochu, což umožňují použité aktuátory (tj. maximální vygenerovaná síla a maximální zdvih během provozu). K optimalizaci systému TMD byl použit numerický model, který reprezentoval rozložení hmotnosti věže a momenty setrvačnosti, jak jsou uvedeny v identifikovaných vlastnostech konstrukce. Prvky tuhosti mezi podlahami byly rovněž přizpůsobeny tak, aby odpovídaly tvarům módů a vlastním frekvencím z pozorování v plném měřítku. Na obr. 6 vlevo jsou znázorněny tvary módů a vlastní frekvence tohoto použitého analogického modelu. Na obr. 6 vlevo jsou také porovnány tvary módů analogického modelu s tvary detailního modelu připraveného poradcem pro konstrukční řešení.


Kromě toho byl realizován diskrétní model TMD jako kyvadlový systém zachycující i jeho excentrickou polohu na věži. Charakteristiky zatížení pro rozhodný vstupní případ, tj. rezonanční buzení způsobené vířením, jsou velmi podobné charakteristikám pro harmonické buzení z jednoho směru. Současné zatížení poryvy větru je však ze své podstaty stochastické (náhodné) povahy a platí pro něj jiná optimalizační kritéria než známé Den Hartogovo kritérium. Kromě toho jsou relativní posuny hmoty TMD větší u stochastického než u harmonického typu zatížení. Vzhledem k tomu, že pro číselné stanovení optimálních parametrů systému TMD je třeba zvažovat zatížení blízké realitě, byl vygenerován časový průběh, který zahrnoval jak stochastické zatížení poryvy (založené na Davenportově spektru), tak superponovanou rezonanční složku podobnou víření, která představuje celkové buzení bočním větrem (viz obr. 3 vpravo). Snížení odchylky věže, kterého lze dosáhnout pomocí optimalizovaného pasivního systému TMD, a výsledné posuny TMD jsou znázorněny na obr. 3 vpravo.
Na základě těchto výsledků pro odhadované vlastní tlumení konstrukce ξ = 0,8 % bylo zjištěno, že pro udržení posunů v rozmezí +/- 650 mm při zachování optimálního poměru tlumení TMD pro nejlepší výkon TMD je nutná hmotnost systému TMD 240 t. Zvýšení tlumení TMD by mohlo zkrátit dráhu, přičemž účinnost by byla stále dostatečná, ale to by nepříznivě ovlivnilo požadavky na sílu aktuátoru. Pro určení potřebných sil pro optimální nastavení 240t systému TMD byl použit také analogický model, který ověřil, že při maximální síle 40 kN z aktuátorů lze dosáhnout vychýlení věže v rozmezí +/- 200 mm. Na obr. 4 jsou zobrazeny výsledky numerické simulace v časové oblasti na analogickém numerickém modelu; v tomto případě jsou zobrazeny výsledné odchylky vrcholu věže, výchylky hmoty TMD a aktivní vstupní síly, které je způsobují.


6.0 Popis systému
Dualita řídicího systému slouží a) ke snížení spotřeby energie při běžném pasivním provozu, aby se snížily vznikající vibrace; b) ke snížení požadavků na sílu pro aktuátory díky využití rezonančních efektů k vybuzení hlavní hmoty TMD, aby nakonec bylo dosaženo skutečné požadované síly. V porovnání s jinými řídicími systémy (viz obr. 1) tedy aktuátory spojují hlavní konstrukci a hmotu systému TMD, ale nepoužívají se k přímému ovládání hmoty TMD, jak by tomu bylo v případě typického systému aktivního systému regulace hmoty (Active Mass Driver)/tlumič.
Pro realizovaný TMD s duálním použitím byla zvolena reakční hmotnost pro pasivní provoz 240 tun. V režimu buzení jsou k TMD připojeny dva lineární pohony – v každém hlavním směru jeden – s čepy v blízkosti těžiště hmoty, aby se zabránilo vzniku torzních odchylek. Každý lineární pohon může vyvinout sílu až 40 kN při zdvihu max. +/- 600 mm (viz detail na obr. 2). Lineární pohony lze odpojit, takže celý pasivní režim nebude ovlivněn ložisky aktuátorů z důvodu zabránění nepravděpodobnému případu poruchy ložisek.


Obrázek 10 – Typy TMD systémů – TMD s duálním použitím v porovnání s pasivními, poloaktivními, aktivními a hybridními systémy
Systém je vybaven čtyřmi jednoosými akcelerometry (seismický K-Beam/MEMS; v každém směru jeden) pro určení zrychlení horní úrovně věže a hmotnosti TMD. Signály zrychlení se filtrují podle pásma uvnitř frekvenčního rozsahu základních přirozených frekvencí věže (0,1–0,3 Hz) a integrují se, aby se získaly rychlosti a odchylky věže.
Kromě toho lze integrované hodnoty posunutí porovnat s hodnotami doplňkového globálního navigačního satelitního systému instalovaného rovněž na vrcholu, aby bylo možné porovnat odchylky signálu. V souladu s tím byly provedeny počáteční korelační testy. Kromě toho se posuny TMD monitorují přímo pomocí snímačů strunového potenciometru a indukčního systému měření délky integrovaného v lineárních motorech.
7.0 Řídicí algoritmus
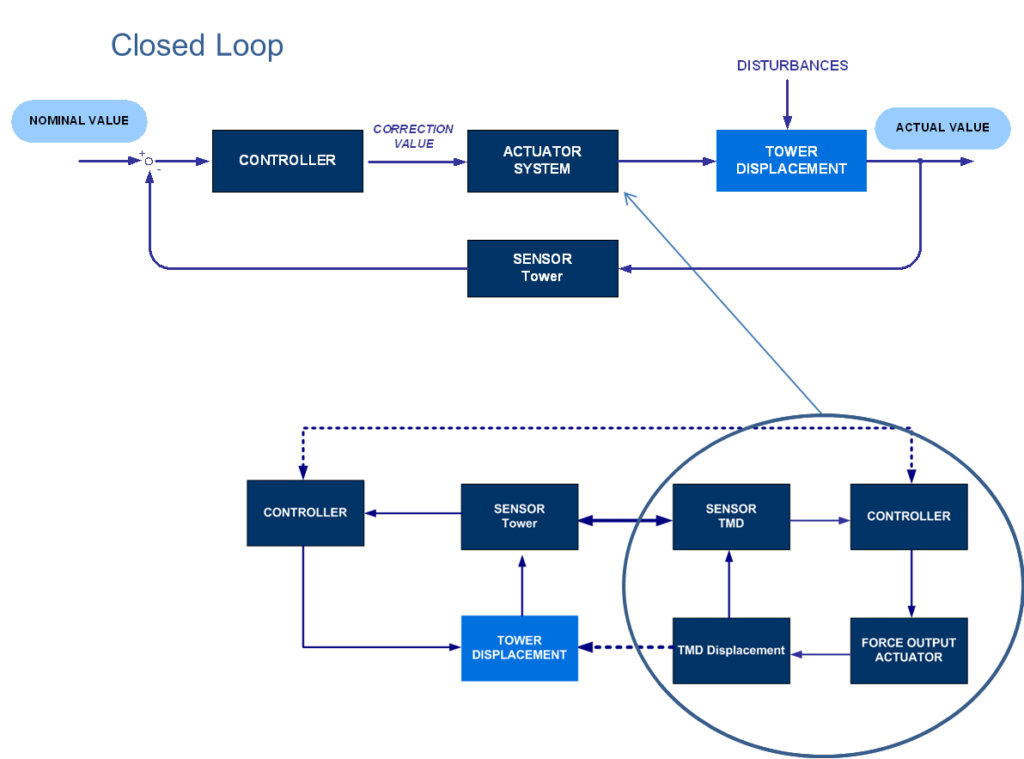
Obecná regulační smyčka pro věž je znázorněna na obr. 5, kde je znázorněna sekvence řízení v uzavřené smyčce. Podrobný návrh řídicího algoritmu by vyžadoval analytické modely interakce mezi akčními a hmotou TMD, aby bylo možné určit souvislost mezi vstupem akčního členu a působící silou. Ty by se měly kombinovat s analytickým modelem hlavní konstrukce, který popisuje celkové dynamické chování budovy. V porovnání se standardními řídicími algoritmy, které byly použity v jiných aplikacích HMD, např. v [2],[3] nebo byly teoreticky zkoumány, např. v [1] Algoritmus pro tuto aplikaci musel pro věž zohlednit synchronní řízené buzení v jednom hlavním směru a snížení vibrací v kolmém směru. Vzhledem k tomu, že dynamická citlivost se očekává především v základních režimech, lze pro obě tyto úlohy použít lineární řízení se zpětnou vazbou se všemi jeho výhodami s ohledem na zamezení nestabilitám. Pro použitou jednoduchou realizaci platí, že lineární systém, který tlumí dynamickou citlivost věže kolmo na buzení, řídí příslušný aktuátor prostřednictvím zadaného váženého lineárního součtu sedmi měření dynamiky konstrukce. Jde o měření: zrychlení TMD a vrcholu věže, rychlosti TMD a vrcholu věže, posuny TMD a vrcholu věže a relativní posun TMD vůči vrcholu věže.
Je důležité poznamenat, že předem zvolené faktory vážení jsou jednoduché, kladné nebo záporné skalární zisky. Parametrizace faktorů vážení vychází z dynamických zkoušek věže a nepoužívá žádné úpravy závislé na frekvenci. Zpětná vazba aktivního aktuátoru se počítá okamžitě (při 50 Hz) a je opět lineární kombinací předchozích dynamických měření. Nepoužívá se žádná nelineární manipulace. Návrh řízení byl také implementován do numerické simulace v časové oblasti (tj. přímá integrace), aby se prokázala výkonnost řízení aktuátoru pro zmírnění vibrací. Pro režim buzení byl použit stejný přístup v kombinaci s posunem měřené konstrukce, který představuje vybuzení věže na požadovanou hodnotu odchylky. Posun je sinusová funkce založená na zjištěné základní frekvenci každého směru. Řídicí výstup pro potlačení změn horního průhybu způsobených jinými narušeními je poté modulován na sinusové funkci posunu a hodnota regulace se odpovídajícím způsobem upraví.

Lineární řízení se zpětnou vazbou pro snížení dynamické citlivosti věže kolmo na buzení umožňuje, aby silový povel pro pohon byl zadaným váženým lineárním součtem sedmi dynamických měření programu. Těchto sedm měření je: zrychlení TMD a věže, rychlost TMD a věže, posun TMD a věže a relativní posun TMD vůči věži. Je důležité poznamenat, že faktory vážení jsou jednoduché, kladné nebo záporné skalární hodnoty. Parametrizace faktoru vážení vychází z experimentálních dynamických zkoušek věže. Zpětná vazba aktuátoru je aktivní, počítá se okamžitě (50 Hz)
a faktory vážení jsou skalární hodnoty, které nepoužívají žádnou formu funkce přenosu závislé na frekvenci. Také zpětná vazba je lineární kombinací dynamické vlastnosti. Nepoužívá se žádná nelineární manipulace an nelinární logika. Návrh řízení byl implementován pro numerickou simulaci v časové oblasti (přímá integrace), takže pro každý časový krok bylo možné přizpůsobit silový vstup do hmoty TMD jako řízení aktuátoru. Na obrázku 12 jsou uvedeny výsledky simulace pro potlačení vibrací – posuny věže a výsledná dráha TMD.


Pro režim buzení byl použit stejný přístup v kombinaci s posunem měřené konstrukce, který představuje vybuzení věže na požadovanou hodnotu odchylky. Posun je sinusová funkce založená na zjištěné základní frekvenci pro každý směr. Řídicí výstup pro potlačení změn horní odchylky způsobené narušením je poté modulován na sinusové funkci
posunu a hodnotu regulace je nutno odpovídajícím způsobem upravit. Pro tento posun experimentálně určen faktor vážení. Na obrázku 13 jsou zobrazeny číselné výsledky s rušivým nárazovým zatížením pro režim buzení s jednoduchým sinusovým buzením a s použitým řídicím algoritmem.


8.0 Koncepce bezpečnosti
Vzhledem k síle +/- 40 kN, kterou mohou vyvinout lineární pohony používané jako akční členy, je nezbytná koncepce bezpečnosti, která zajistí, že posuny věže nepřekročí ustanovení ohledně únavy konstrukce a materiálu. To platí i přesto, že výstupní síla není dostatečná k tomu, aby způsobila odchylku horní části větší než předem stanovených +/-200 mm. Jedním z přístupů ke zvýšení bezpečnosti systému bylo zvýšení redundance monitorovacích snímačů, které zaznamenávají průhyb horní části věže. Toho lze nejlépe dosáhnout implementací dalšího nezávislého monitorovacího systému, který v ideálním případě používá jiný měřicí princip než vlastní řídicí hardware. Pro zde prezentovaný projekt byly v řídicím hardwaru použity akcelerometry a definovaný práh zrychlení pro pásmovou filtraci signálu v rozsahu příslušných přirozených frekvencí konstrukce. Nadřazeným monitorovacím systémem je globální družicový navigační systém (GNSS) s přesností +/- 10 mm. Monitorovací systém GNNS vyžaduje referenční základnovou stanici, která zpracovává souřadnicová data na skutečné hodnoty odezvy na posun. Pokud odchylka vrcholu věže během režimu umělého buzení překročí předem stanovenou mez, což by mohlo být způsobeno dalším větrem nebo jiným buzením, relé přepne signál detekce přítomnosti na 0 V. To způsobí přerušení režimu buzení. Kromě toho oba monitorovací systémy neustále kontrolují získaná data, zda nedošlo k výskytu chybných signálů ze snímačů, což rovněž vede k přerušení aktivního režimu buzení. Chybné signály zrychlení / strunového potenciometru budou detekovány pomocí kritéria výběru spektrálních špiček – pouze pokud lze možné vybrat špičku v příslušném rozsahu, lze předpokládat, že snímače poskytují legitimní signály. Monitorovací systém GNNS analyzuje změnu souřadnicových dat, ovšem pokud se vzorkovaná data včas nezmění, automaticky se předpokládá chybný signál.
9.0 Vibrační zkoušky
Počáteční vibrační zkoušky věže byly provedeny v současné fázi, kdy věž ještě není dokončena, takže základní frekvence věže v této fázi jsou nad stanoveným rozsahem ladění pasivního systému TMD. Systém TMD je nastaven na nejvyšší možnou frekvenci ladění. Cílem vibračních zkoušek bylo stanovení základních frekvencí věže se zablokovaným systémem TMD a vlastního tlumení konstrukce. Dále by se mělo stanovit dynamické chování s aktivovaným pasivním systémem TMD a zvýšení tlumení konstrukce vlivem pasivního systému TMD. K určení základních přirozených frekvencí věže lze použít metodu zprůměrované normalizované spektrální hustoty výkonu [1] (ANPSD). Za tímto účelem je zaznamenané časové průběhy nutno rozdělit do segmentů. Tyto segmenty je nutno převést do frekvenční oblasti. Výsledná spektra je nutno normalizovat, zprůměrovat a vynásobit komplexně konjugovanými spektry.
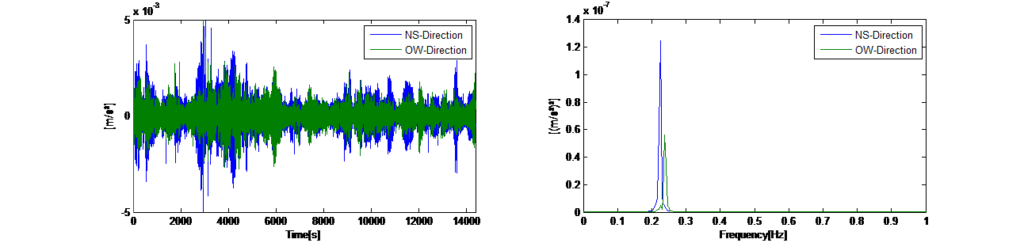
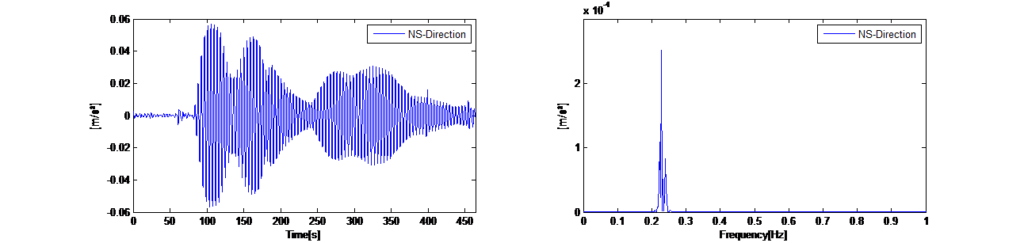
Tím se odstraní všechny náhodné vibrace a ve zprůměrovaném spektru se zobrazí pouze opakující se volné vibrace konstrukce, které nyní představují dominantně buzené přirozené frekvence věže. Na obrázku 14 vlevo jsou zobrazeny zaznamenané časové průběhy vodorovných vibrací okolí ve směrech x a y při zablokovaném systému TMD. Na obrázku 14 vlevo jsou zobrazena výsledná zprůměrovaná automatická spektra výkonu pro úsek o délce 120 sekund. Spektra ukazují, že věž vykazuje dynamickou odezvu ve dvou dominantních frekvencích (0,225 Hz ve směru x a 0,245 Hz ve směru y).
V návaznosti na výše popsanou metodu zprůměrovaného spektra výkonu – která předpokládá, že okolní buzení způsobuje dostatečnou dynamickou odezvu v zájmových módech vibrací, aby bylo dosaženo stochastické bezpečnosti – byly vlastní frekvence určeny pomocí komerčního softwaru pro zpracování signálů ARTEMIS, [1] který zahrnuje metody rozšířené dekompozice frekvenční oblasti a stochastické identifikace podprostoru.

Metody rozšířená dekompozice ve frekvenční oblasti (EFDD) a stochastické identifikace podprostoru jsou široce používané techniky pro identifikaci modálních parametrů výhradně na výstupu.


Metoda EFDD je založena na výpočtu spekter odezvy. Pro udržení nízké úrovně chyby odhadu spektra a spolehlivou extrakci modálních parametrů jsou proto nutné dlouhé záznamy. K identifikaci mostů pomocí modelu založeného výhradně na výstupu byl použit algoritmus stochastické identifikace podprostoru. Metody stochastické identifikace podprostoru fungují v časové oblasti a jsou založeny na popisu dynamického problému ve stavovém prostoru. Výsledky identifikace systému při různých řádech modelu se porovnávají za účelem rozlišení skutečných strukturálních módů od falešných módů v tzv. stabilizačních diagramech. Tyto diagramy jsou oblíbeným způsobem výběru identifikovaného modelu systému, protože skutečné strukturální módy mají tendenci být stabilní pro po sobě následující pořadí modelu a splňují určitá stabilizační kritéria, která se vyhodnocují automatizovaným postupem. Na obrázku 15 je zobrazena výsledná karta stability pro zaznamenaná data z okolí, z níž bylo možné určit příslušné módy. Identifikované módy a stanovené poměry tlumení pro jednotlivé módy ve stavu se zablokovaným systémem TMD (vlevo) a se zapnutým systémem TMD (vpravo) jsou rovněž zobrazeny na obrázku 14. Je patrné zvýšení tlumení konstrukce. Dodatečné tlumení konstrukce se pohybuje v rozmezí teoretické hodnoty, kterou lze určit z teoretického modelu, pro který bylo uvažováno nevyladěné nastavení systému TMD.
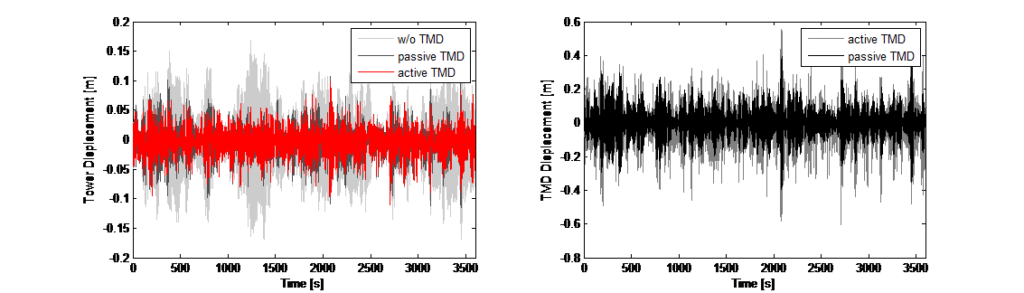
Kromě testů okolních vibrací s pasivním systémem TMD byly provedeny předběžné testy s aktivním režimem buzení, a to i přes nevyladěný stav systému TMD. Obrázek 12 vlevo ukazuje časový průběh zaznamenaných zrychlení na vrcholu věže. Po počátečním sinusovém buzení bylo možné pomocí algoritmu pro ustálenou úroveň zrychlení experimentálně určit korelaci mezi průhybem věže a nuceným posunem hmoty systému TMD. Časový průběh na obrázku 12 zobrazuje oba zkušební scénáře v režimu buzení a odpovídající spektra FFT ukazují jasnou odezvu věže v jejích dvou základních frekvencích (směr x a y). Zeleně vyznačený časový úsek představuje sinusové buzení hmoty s vypnutým aktivním řízením, které způsobilo dynamickou odezvu v obou hlavních směrech. Výsledné spektrum FFT zobrazuje dvě špičky pro identifikaci základních frekvencí v těchto dvou směrech. Modře vyznačený časový úsek je pro buzení s povoleným aktivním řízením, které způsobilo stabilnější posun věže převážně v jednom směru. Výsledný útlum vibrací po vypnutí režimu buzení byl rovněž použit k určení tlumení konstrukce a byl stanoven na D = 2,4 %. Tento výsledek koreluje s poměrem tlumení určeným pomocí algoritmů SSI.

10.0 Závěr a výhled
Ve 246 m vysoké zkušební věži Thyssen Krupp byl instalován systém TMD s duálním použitím, jehož cílem je úmyslně vybuzovat věž na řízenou dynamickou odezvu v jejích základních frekvencích. Cílem tohoto buzení je dosáhnout definovaných výkyvů budovy ve dvou hlavních směrech věže. Na základě numerických výpočtů bylo zjištěno, že k dosažení požadovaného přídavného tlumení pro pasivní režim a k vytvoření požadované řídicí síly pro dosažení posunu vrcholu věže +/- 200 mm je zapotřebí systém TMD 240 t. Pro vytvoření ustálené úrovně posunu pro režim buzení a potlačení posunů způsobených větrem a vynucenou složkou vibrací v kolmém směru byl vyvinut řídicí algoritmus, který byl testován s použitím numerických simulací. Po instalaci pasivního systému TMD kyvadlového typu, pro který byly jako reakční hmota použity prefabrikované betonové desky, byly aktuátory uvedeny do provozu a byly provedeny první zkoušky. Zkoušky ukázaly, že vlastní tlumení věže je vyšší, než se předpokládalo, ale že lze jasně určit všechny relevantní módy. Aktivní režim buzení budovy funguje a bylo ho možno otestovat, i když nikoli v plném rozsahu, aby bylo možné odvodit všechny provozní parametry, protože budova ještě není zcela dokončena. Vzhledem k nedokončenosti budovy nebylo možno přizpůsobit pasivní systém TMD stanoveným základním frekvencím.
Jakmile bude systém TMD upraven, budou provedeny další zkoušky budovy, které budou zahrnovat také zkoušky amplitudově závislých tlumicích vlastností a integrity koncepce bezpečnosti.
REFERENCE
[1] Wenzel, H., Pichler, D., Schedler, R. (1991). „Ambiente Schwingungsmessungen zur System und Schadenserkennung an Tragwerken“, Bauingenieur 74
[2] Döhler, M., Andersen, P.: Mevel, L. (2012). „Operational Modal Analysis using a Fast Stochastic Subspace Identification Method“, Sborník z řady konferencí Společnosti pro experimentální mechaniku (Society for Experimental Mechanics)
[3] Soong, T. T., Spencer, J. R. (2000). „Active, Semi-Active and hybrid control of structures“ na 12. světové konferenci pro zemětřesné inženýrství
[4] Ricciardelli, F.; Pizzimenti, A.D.; Mattei, M. (2003). Pasivní i aktivní TMD jako řešení větrných podmínek výškových staveb. Eng. Struct., 25, 1199–1209
[5] Yang, N.Y.; Agrawal, A.K.; Samali, B.; Wu, J.C. Benchmark Problem for Response Control of Wind-Excited Tall Buildings. J. Eng. Mech. 2004, 130, 437–446.
[6] Watakabe, M.; Tohdp, M.; Chiba, O.; Izumi, N.; Ebisawa, H.; Fujita, T. Response control performance of a hybrid mass damper applied to a tall building. Earthq. Eng. Struct. Dyn. 2001, 30, 1655–1676.
[7] Tan, P.; Liu, Y.; Zhou, F.; Teng, J. Hybrid Mass Dampers for Canton Tower. CTBUH J. 2012, 24–29.
[8] Soong, T. T. „Active Structural Control: Theory and Practice“; John Wiley & Sons, Inc.: New York, NY, USA, 1990
[9] Preumont, A., Kazuto, S. (2008). „Active Control of Structures“, Wiley, Padstow
1.0 Úvod/ Historie
V jihozápadním Německu byla postavena 246 metrů vysoká věž, která má sloužit jako zkušební zařízení pro inovace výtahů. Věž má kruhový půdorys o průměru 20 m a poskytuje prostor pro 9 šachet pro zkoušky výtahů, požární výtah a prosklený panoramatický výtah. Kromě toho je k dispozici 220 m šachta, která se používá jako šachta pro mechanické zvedání pro zajištění zkušebních programů.
Základna věže má průměr 40 m, aby poskytla další prostor pro servisní zázemí, vstupní halu a vzdělávací centrum. Vyhlídková plošina ve výšce 232 m – nejvyšší na území Německa – umožňuje nádherný výhled na Černý les a za jasného počasí i na Alpy.

2.0 Konstrukční systém
Konstrukční systém zkušební věže představuje v zásadě železobetonový tubus o průměru 20,8 m, který je upnut 30 metrů do okolní zeminy (viz obrázek 2). Do úrovně 110 m má tubus tloušťku stěn 40 cm a nad ní 25 cm. Zemina, tvořená vrstvou keuperu a pod ní ležícím skořápkovým vápencem, poskytuje vysokou únosnost, takže nebylo nutné použít pilotové založení. Kromě sevření okolní půdou poskytuje širší základová konstrukce věže dodatečnou příčnou tuhost.
Vnitřní vyztužení betonového tubusu je důsledkem především vnitřních stěn výtahových šachet. Pouze na některých výškových úrovních byly nainstalovány prefabrikované stropní desky, aby byl umožněn přístup k výtahovým šachtám. Některé výtahové šachty končí ve výšce 115 m a jsou zakryty 40 cm silnými podlahami s dlouhým rozpětím, které byly odlity přímo na místě. Tyto podlahy se používají v kancelářských prostorách. Nad nimi se nachází prázdný prostor do výšky 197 m, který slouží jako zásobník tepla a pro systém TMD. V horní části věže jsou kancelářské prostory a zbývající výtahové šachty.

Charakteristickým rysem testovací věže je textilní fasáda, kterou tvoří síťovina ze skelných vláken potažená PTFE. Šířka otvorů síťoviny se s výškou budovy zvětšuje, aby se zvýšila průsvitnost fasády, snížila hustota a hmotnost materiálu a posílily se aerodynamické účinky.
Spirálovitý tvar fasády má fungovat jako tzv. Scrutonova spirála a samotná tkanina pomáhá stínit betonovou konstrukci, aby se zabránilo tepelnému namáhání způsobenému slunečním zářením. Při návrhu fasády a výběru materiálu bylo třeba zohlednit aspekty instalace, údržby a trvanlivosti, ovšem navíc i zatížení větrem.
3.0 Postup výstavby

Stavba zkušební věže proběhla v následujících krocích:
- Vyhloubení 30 m hluboké kruhové stavební jámy pro základnu věže. Výkopu a jeho tvaru bylo dosaženo odstřelem na začátku. Po výkopu byla jáma zajištěna zemními kotvami a ostěním ze vstřikovaného betonu.
- Vylití roštových základů
- Výstavba svislé betonové konstrukce s použitím posuvného bednění. Všechny stěny se stavěly nepřetržitě po dobu 4 měsíců.
- Výstavba podlahových desek
- Výstavba vstupního prostoru
4.0 Předpokládaná dynamická citlivost na zatížení větrem
Základní frekvence pro zkušební věž byly předpokládány v rozmezí 0,17– 0,20 Hz v závislosti na fázi výstavby a stavu betonu (popraskaný/nepopraskaný) – viz obrázek 4.

Analýza větru ukázala, že k rezonančnímu buzení konstrukce může docházet při rychlostech větru, které odpovídají hodnotám při zemi (výška 10 m) v rozmezí 55–60 km/h. Předpokládalo se, že bez dodatečného tlumení by toto rezonanční buzení způsobilo odchylky horní části věže přibližně +/- 750 mm, což by nejen způsobilo nepohodlí uživatelům, ale mělo by to také významné důsledky pro únavovou životnost betonové konstrukce věže (viz obrázek 5). Z důvodu snížení dynamické citlivosti na boční vítr byl realizován pasivní systém tlumiče vibrací. Vzhledem k tomu, že věž má být používána jako zkušební věž pro výtahová zařízení citlivá na kývání, hledal vlastník možnost, jak věž vybudit uměle v klidných dnech, avšak s posunem, který by nezpůsobil žádné problémy s únavou konstrukce či materiálu. Požadovaná úroveň umělého kývavého pohybu se pohybovala v bezpečném rozmezí, přibližně +/- 200 mm. Tento požadavek poskytl vzácnou příležitost realizovat hybridní systém tlumiče hmotností (HMD) nebo, protože se konstrukční systém odchyluje od jiných systémů HMD, které byly vyrobeny v minulosti, takzvaný systém TMD s duálním použitím. Systém bude představen v následujících kapitolách, včetně optimalizace pasivního systému, návrhu mechanismu aktuátorů, řídicích algoritmů a koncepce bezpečnosti.

5.0 Optimalizace pasivního systému tlumiče vibrací
Parametry pasivního systému TMD musely být stanoveny s ohledem na tři různé aspekty: a) zajištění dostatečného dodatečného tlumení konstrukce, aby se snížila dynamická citlivost v důsledku buzení víry; b) omezení výsledný posun hlavní hmoty TMD v pasivním režimu na dosažitelnou/praktickou hodnotu při buzení nárazovým větrem a c) zvolení hmoty TMD podle příkonu energie, který je nutný pro požadovaný maximální odklon věže v režimu buzení, s ohledem na její účinnou plochu, což umožňují aktuátory (tj. maximální vygenerovaná síla a maximální zdvih během provozu). K optimalizaci systému TMD byl použit numerický model, který reprezentoval rozložení hmotnosti věže a momenty setrvačnosti, jak jsou uvedeny v identifikovaných vlastnostech konstrukce. Prvky tuhosti mezi podlahami byly rovněž přizpůsobeny tak, aby odpovídaly tvarům módů a vlastním frekvencím z pozorování v plném měřítku. Na obr. 6 vlevo jsou znázorněny tvary módů a vlastní frekvence tohoto použitého analogického modelu. Na obr. 6 vlevo jsou také porovnány tvary módů analogického modelu s tvary detailního modelu připraveného poradcem pro konstrukční řešení.


Kromě toho byl realizován diskrétní model TMD jako kyvadlový systém zachycující i jeho excentrickou polohu na věži. Charakteristiky zatížení pro rozhodný vstupní případ, tj. rezonanční buzení způsobené vířením, jsou velmi podobné charakteristikám pro harmonické buzení z jednoho směru. Současné zatížení poryvy větru je však ze své podstaty stochastické (náhodné) povahy a platí pro něj jiná optimalizační kritéria než známé Den Hartogovo kritérium. Kromě toho jsou relativní posuny hmoty TMD větší u stochastického než u harmonického typu zatížení. Vzhledem k tomu, že pro číselné stanovení optimálních parametrů systému TMD je třeba zvažovat zatížení blízké realitě, byl vygenerován časový průběh, který zahrnoval jak stochastické zatížení poryvy (založené na Davenportově spektru), tak superponovanou rezonanční složku podobnou víření, která představuje celkové buzení bočním větrem (viz obr. 3 vpravo). Snížení odchylky věže, kterého lze dosáhnout pomocí optimalizovaného pasivního systému TMD, a výsledné posuny TMD jsou znázorněny na obr. 3 vpravo. Na základě těchto výsledků pro odhadované vlastní tlumení konstrukce ξ = 0,8 % bylo zjištěno, že pro udržení posunů v rozmezí +/- 650 mm při zachování optimálního poměru tlumení TMD pro nejlepší výkon TMD je nutná hmotnost systému TMD 240 t. Zvýšení tlumení TMD by mohlo zkrátit dráhu, přičemž účinnost by byla stále dostatečná, ale to by nepříznivě ovlivnilo požadavky na sílu aktuátoru. Pro určení potřebných sil pro optimální nastavení 240t systému TMD byl použit také analogický model, který ověřil, že při maximální síle 40 kN z aktuátorů lze dosáhnout vychýlení věže v rozmezí +/- 200 mm. Na obr. 4 jsou zobrazeny výsledky numerické simulace v časové oblasti na analogickém numerickém modelu; v tomto případě jsou zobrazeny výsledné odchylky vrcholu věže, výchylky hmoty TMD a aktivní vstupní síly, které je způsobují.


6.0 Popis systému
Dualita řídicího systému slouží a) ke snížení spotřeby energie při běžném pasivním provozu, aby se snížily vznikající vibrace; b) ke snížení požadavků na sílu pro aktuátory díky využití rezonančních efektů k vybuzení hlavní hmoty TMD, aby nakonec bylo dosaženo skutečné požadované síly. V porovnání s jinými řídicími systémy (viz obr. 1) tedy aktuátory spojují hlavní konstrukci a hmotu systému TMD, ale nepoužívají se k přímému ovládání hmoty TMD, jak by tomu bylo v případě typického systému aktivního systému regulace hmoty (Active Mass Driver)/tlumič. Pro realizovaný TMD s duálním použitím byla zvolena reakční hmotnost pro pasivní provoz 240 tun. V režimu buzení jsou k TMD připojeny dva lineární pohony – v každém hlavním směru jeden – s čepy v blízkosti těžiště hmoty, aby se zabránilo vzniku torzních odchylek. Každý lineární pohon může vyvinout sílu až 40 kN při zdvihu max. +/- 600 mm (viz detail na obr. 2). Lineární pohony lze odpojit, takže celý pasivní režim nebude ovlivněn ložisky aktuátorů z důvodu zabránění nepravděpodobnému případu poruchy ložisek.


Systém je vybaven čtyřmi jednoosými akcelerometry (seismický K-Beam/MEMS; v každém směru jeden) pro určení zrychlení horní úrovně věže a hmotnosti TMD. Signály zrychlení se filtrují podle pásma uvnitř frekvenčního rozsahu základních přirozených frekvencí věže (0,1–0,3 Hz) a integrují se, aby se získaly rychlosti a odchylky věže. Kromě toho lze integrované hodnoty posunutí porovnat s hodnotami doplňkového globálního navigačního satelitního systému instalovaného rovněž na vrcholu, aby bylo možné porovnat odchylky signálu. V souladu s tím byly provedeny počáteční korelační testy. Kromě toho se posuny TMD monitorují přímo pomocí snímačů strunového potenciometru a indukčního systému měření délky integrovaného v lineárních motorech.
7.0 Řídicí algoritmus
Obecná regulační smyčka pro věž je znázorněna na obr. 5, kde je znázorněna sekvence řízení v uzavřené smyčce. Podrobný návrh řídicího algoritmu by vyžadoval analytické modely interakce mezi akčními a hmotou TMD, aby bylo možné určit souvislost mezi vstupem akčního členu a působící silou. Ty by se měly kombinovat s analytickým modelem hlavní konstrukce, který popisuje celkové dynamické chování budovy. V porovnání se standardními řídicími algoritmy, které byly použity v jiných aplikacích HMD, např. v [2],[3] nebo byly teoreticky zkoumány, např. v [1] Algoritmus pro tuto aplikaci musel pro věž zohlednit synchronní řízené buzení v jednom hlavním směru a snížení vibrací v kolmém směru. Vzhledem k tomu, že dynamická citlivost se očekává především v základních režimech, lze pro obě tyto úlohy použít lineární řízení se zpětnou vazbou se všemi jeho výhodami s ohledem na zamezení nestabilitám. Pro použitou jednoduchou realizaci platí, že lineární systém, který tlumí dynamickou citlivost věže kolmo na buzení, řídí příslušný aktuátor prostřednictvím zadaného váženého lineárního součtu sedmi měření dynamiky konstrukce. Jde o měření: zrychlení TMD a vrcholu věže, rychlosti TMD a vrcholu věže, posuny TMD a vrcholu věže a relativní posun TMD vůči vrcholu věže. Je důležité poznamenat, že předem zvolené faktory vážení jsou jednoduché, kladné nebo záporné skalární zisky. Parametrizace faktorů vážení vychází z dynamických zkoušek věže a nepoužívá žádné úpravy závislé na frekvenci. Zpětná vazba aktivního aktuátoru se počítá okamžitě (při 50 Hz) a je opět lineární kombinací předchozích dynamických měření. Nepoužívá se žádná nelineární manipulace. Návrh řízení byl také implementován do numerické simulace v časové oblasti (tj. přímá integrace), aby se prokázala výkonnost řízení aktuátoru pro zmírnění vibrací. Pro režim buzení byl použit stejný přístup v kombinaci s posunem měřené konstrukce, který představuje vybuzení věže na požadovanou hodnotu odchylky. Posun je sinusová funkce založená na zjištěné základní frekvenci každého směru. Řídicí výstup pro potlačení změn horního průhybu způsobených jinými narušeními je poté modulován na sinusové funkci posunu a hodnota regulace se odpovídajícím způsobem upraví.

Lineární řízení se zpětnou vazbou pro snížení dynamické citlivosti věže kolmo na buzení umožňuje, aby silový povel pro pohon byl zadaným váženým lineárním součtem sedmi dynamických měření programu. Těchto sedm měření je: zrychlení TMD a věže, rychlost TMD a věže, posun TMD a věže a relativní posun TMD vůči věži. Je důležité poznamenat, že faktory vážení jsou jednoduché, kladné nebo záporné skalární hodnoty. Parametrizace faktoru vážení vychází z experimentálních dynamických zkoušek věže. Zpětná vazba aktuátoru je aktivní, počítá se okamžitě (50 Hz) a faktory vážení jsou skalární hodnoty, které nepoužívají žádnou formu funkce přenosu závislé na frekvenci. Také zpětná vazba je lineární kombinací dynamické vlastnosti. Nepoužívá se žádná nelineární manipulace an nelinární logika. Návrh řízení byl implementován pro numerickou simulaci v časové oblasti (přímá integrace), takže pro každý časový krok bylo možné přizpůsobit silový vstup do hmoty TMD jako řízení aktuátoru. Na obrázku 12 jsou uvedeny výsledky simulace pro potlačení vibrací – posuny věže a výsledná dráha TMD.


Pro režim buzení byl použit stejný přístup v kombinaci s posunem měřené konstrukce, který představuje vybuzení věže na požadovanou hodnotu odchylky. Posun je sinusová funkce založená na zjištěné základní frekvenci pro každý směr. Řídicí výstup pro potlačení změn horní odchylky způsobené narušením je poté modulován na sinusové funkci posunu a hodnotu regulace je nutno odpovídajícím způsobem upravit. Pro tento posun experimentálně určen faktor vážení. Na obrázku 13 jsou zobrazeny číselné výsledky s rušivým nárazovým zatížením pro režim buzení s jednoduchým sinusovým buzením a s použitým řídicím algoritmem.


8.0 Koncepce bezpečnosti
Vzhledem k síle +/- 40 kN, kterou mohou vyvinout lineární pohony používané jako akční členy, je nezbytná koncepce bezpečnosti, která zajistí, že posuny věže nepřekročí ustanovení ohledně únavy konstrukce a materiálu. To platí i přesto, že výstupní síla není dostatečná k tomu, aby způsobila odchylku horní části větší než předem stanovených +/-200 mm. Jedním z přístupů ke zvýšení bezpečnosti systému bylo zvýšení redundance monitorovacích snímačů, které zaznamenávají průhyb horní části věže. Toho lze nejlépe dosáhnout implementací dalšího nezávislého monitorovacího systému, který v ideálním případě používá jiný měřicí princip než vlastní řídicí hardware. Pro zde prezentovaný projekt byly v řídicím hardwaru použity akcelerometry a definovaný práh zrychlení pro pásmovou filtraci signálu v rozsahu příslušných přirozených frekvencí konstrukce. Nadřazeným monitorovacím systémem je globální družicový navigační systém (GNSS) s přesností +/- 10 mm. Monitorovací systém GNNS vyžaduje referenční základnovou stanici, která zpracovává souřadnicová data na skutečné hodnoty odezvy na posun. Pokud odchylka vrcholu věže během režimu umělého buzení překročí předem stanovenou mez, což by mohlo být způsobeno dalším větrem nebo jiným buzením, relé přepne signál detekce přítomnosti na 0 V. To způsobí přerušení režimu buzení. Kromě toho oba monitorovací systémy neustále kontrolují získaná data, zda nedošlo k výskytu chybných signálů ze snímačů, což rovněž vede k přerušení aktivního režimu buzení. Chybné signály zrychlení / strunového potenciometru budou detekovány pomocí kritéria výběru spektrálních špiček – pouze pokud lze možné vybrat špičku v příslušném rozsahu, lze předpokládat, že snímače poskytují legitimní signály. Monitorovací systém GNNS analyzuje změnu souřadnicových dat, ovšem pokud se vzorkovaná data včas nezmění, automaticky se předpokládá chybný signál.
9.0 Vibrační zkoušky
Počáteční vibrační zkoušky věže byly provedeny v současné fázi, kdy věž ještě není dokončena, takže základní frekvence věže v této fázi jsou nad stanoveným rozsahem ladění pasivního systému TMD. Systém TMD je nastaven na nejvyšší možnou frekvenci ladění. Cílem vibračních zkoušek bylo stanovení základních frekvencí věže se zablokovaným systémem TMD a vlastního tlumení konstrukce. Dále by se mělo stanovit dynamické chování s aktivovaným pasivním systémem TMD a zvýšení tlumení konstrukce vlivem pasivního systému TMD. K určení základních přirozených frekvencí věže lze použít metodu zprůměrované normalizované spektrální hustoty výkonu [1] (ANPSD). Za tímto účelem je zaznamenané časové průběhy nutno rozdělit do segmentů. Tyto segmenty je nutno převést do frekvenční oblasti. Výsledná spektra je nutno normalizovat, zprůměrovat a vynásobit komplexně konjugovanými spektry.
Tím se odstraní všechny náhodné vibrace a ve zprůměrovaném spektru se zobrazí pouze opakující se volné vibrace konstrukce, které nyní představují dominantně buzené přirozené frekvence věže. Na obrázku 14 vlevo jsou zobrazeny zaznamenané časové průběhy vodorovných vibrací okolí ve směrech x a y při zablokovaném systému TMD. Na obrázku 14 vlevo jsou zobrazena výsledná zprůměrovaná automatická spektra výkonu pro úsek o délce 120 sekund. Spektra ukazují, že věž vykazuje dynamickou odezvu ve dvou dominantních frekvencích (0,225 Hz ve směru x a 0,245 Hz ve směru y).
V návaznosti na výše popsanou metodu zprůměrovaného spektra výkonu – která předpokládá, že okolní buzení způsobuje dostatečnou dynamickou odezvu v zájmových módech vibrací, aby bylo dosaženo stochastické bezpečnosti – byly vlastní frekvence určeny pomocí komerčního softwaru pro zpracování signálů ARTEMIS, [1] který zahrnuje metody rozšířené dekompozice frekvenční oblasti a stochastické identifikace podprostoru.

Metody rozšířená dekompozice ve frekvenční oblasti (EFDD) a stochastické identifikace podprostoru jsou široce používané techniky pro identifikaci modálních parametrů výhradně na výstupu.


Metoda EFDD je založena na výpočtu spekter odezvy. Pro udržení nízké úrovně chyby odhadu spektra a spolehlivou extrakci modálních parametrů jsou proto nutné dlouhé záznamy. K identifikaci mostů pomocí modelu založeného výhradně na výstupu byl použit algoritmus stochastické identifikace podprostoru. Metody stochastické identifikace podprostoru fungují v časové oblasti a jsou založeny na popisu dynamického problému ve stavovém prostoru. Výsledky identifikace systému při různých řádech modelu se porovnávají za účelem rozlišení skutečných strukturálních módů od falešných módů v tzv. stabilizačních diagramech. Tyto diagramy jsou oblíbeným způsobem výběru identifikovaného modelu systému, protože skutečné strukturální módy mají tendenci být stabilní pro po sobě následující pořadí modelu a splňují určitá stabilizační kritéria, která se vyhodnocují automatizovaným postupem. Na obrázku 15 je zobrazena výsledná karta stability pro zaznamenaná data z okolí, z níž bylo možné určit příslušné módy. Identifikované módy a stanovené poměry tlumení pro jednotlivé módy ve stavu se zablokovaným systémem TMD (vlevo) a se zapnutým systémem TMD (vpravo) jsou rovněž zobrazeny na obrázku 14. Je patrné zvýšení tlumení konstrukce. Dodatečné tlumení konstrukce se pohybuje v rozmezí teoretické hodnoty, kterou lze určit z teoretického modelu, pro který bylo uvažováno nevyladěné nastavení systému TMD. Kromě testů okolních vibrací s pasivním systémem TMD byly provedeny předběžné testy s aktivním režimem buzení, a to i přes nevyladěný stav systému TMD. Obrázek 12 vlevo ukazuje časový průběh zaznamenaných zrychlení na vrcholu věže. Po počátečním sinusovém buzení bylo možné pomocí algoritmu pro ustálenou úroveň zrychlení experimentálně určit korelaci mezi odchylkou věže a nuceným posunem hmoty systému TMD. Časový průběh na obrázku 12 zobrazuje oba zkušební scénáře v režimu buzení a odpovídající spektra FFT ukazují jasnou odezvu věže v jejích dvou základních frekvencích (směr x a y). Zeleně vyznačený časový úsek představuje sinusové buzení hmoty s vypnutým aktivním řízením, které způsobilo dynamickou odezvu v obou hlavních směrech. Výsledné spektrum FFT zobrazuje dvě špičky pro identifikaci základních frekvencí v těchto dvou směrech. Modře vyznačený časový úsek je pro buzení s povoleným aktivním řízením, které způsobilo stabilnější posun věže převážně v jednom směru. Výsledný útlum vibrací po vypnutí režimu buzení byl rovněž použit k určení tlumení konstrukce a byl stanoven na D = 2,4 %. Tento výsledek koreluje s poměrem tlumení určeným pomocí algoritmů SSI.

10.0 Závěr a výhled
Ve 246 m vysoké zkušební věži Thyssen Krupp byl instalován systém TMD s duálním použitím, jehož cílem je úmyslně vybuzovat věž na řízenou dynamickou odezvu v jejích základních frekvencích. Cílem tohoto buzení je dosáhnout definovaných výkyvů budovy ve dvou hlavních směrech věže. Na základě numerických výpočtů bylo zjištěno, že k dosažení požadovaného přídavného tlumení pro pasivní režim a k vytvoření požadované řídicí síly pro dosažení posunu vrcholu věže +/- 200 mm je zapotřebí systém TMD 240 t. Pro vytvoření ustálené úrovně posunu pro režim buzení a potlačení posunů způsobených větrem a vynucenou složkou vibrací v kolmém směru byl vyvinut řídicí algoritmus, který byl testován s použitím numerických simulací. Po instalaci pasivního systému TMD kyvadlového typu, pro který byly jako reakční hmota použity prefabrikované betonové desky, byly aktuátory uvedeny do provozu a byly provedeny první zkoušky. Zkoušky ukázaly, že vlastní tlumení věže je vyšší, než se předpokládalo, ale že lze jasně určit všechny relevantní módy. Aktivní režim buzení budovy funguje a bylo ho možno otestovat, i když nikoli v plném rozsahu, aby bylo možné odvodit všechny provozní parametry, protože budova ještě není zcela dokončena. Vzhledem k nedokončenosti budovy nebylo možno přizpůsobit pasivní systém TMD stanoveným základním frekvencím.
Jakmile bude systém TMD upraven, budou provedeny další zkoušky budovy, které budou zahrnovat také zkoušky amplitudově závislých tlumicích vlastností a integrity koncepce bezpečnosti.
REFERENCE
[1] Wenzel, H., Pichler, D., Schedler, R. (1991). „Ambiente Schwingungsmessungen zur System und Schadenserkennung an Tragwerken“, Bauingenieur 74
[2] Döhler, M., Andersen, P.: Mevel, L. (2012). „Operational Modal Analysis using a Fast Stochastic Subspace Identification Method“, Sborník z řady konferencí Společnosti pro experimentální mechaniku (Society for Experimental Mechanics)
[3] Soong, T. T., Spencer, J. R. (2000). „Active, Semi-Active and hybrid control of structures“ na 12. světové konferenci pro zemětřesné inženýrství
[4] Ricciardelli, F.; Pizzimenti, A.D.; Mattei, M. (2003). Pasivní i aktivní TMD jako řešení větrných podmínek výškových staveb. Eng. Struct., 25, 1199–1209
[5] Yang, N.Y.; Agrawal, A.K.; Samali, B.; Wu, J.C. Benchmark Problem for Response Control of Wind-Excited Tall Buildings. J. Eng. Mech. 2004, 130, 437–446.
[6] Watakabe, M.; Tohdp, M.; Chiba, O.; Izumi, N.; Ebisawa, H.; Fujita, T. Response control performance of a hybrid mass damper applied to a tall building. Earthq. Eng. Struct. Dyn. 2001, 30, 1655–1676.
[7] Tan, P.; Liu, Y.; Zhou, F.; Teng, J. Hybrid Mass Dampers for Canton Tower. CTBUH J. 2012, 24–29.
[8] Soong, T. T. „Active Structural Control: Theory and Practice“; John Wiley & Sons, Inc.: New York, NY, USA, 1990
[9] Preumont, A., Kazuto, S. (2008). „Active Control of Structures“, Wiley, Padstow
Sdílet tento příspěvek
Další zdroje
Potřebujete další informace o tomto tématu?
Neváhejte se na nás obrátit s konkrétním dotazem.
Jeden z našich projektových inženýrů se vám brzy ozve.
Další zdroje
Potřebujete další informace o tomto tématu?
Neváhejte se na nás obrátit s konkrétním dotazem.
Jeden z našich projektových inženýrů se vám brzy ozve.